二分搜索树
二分搜索树
一、概念及其介绍
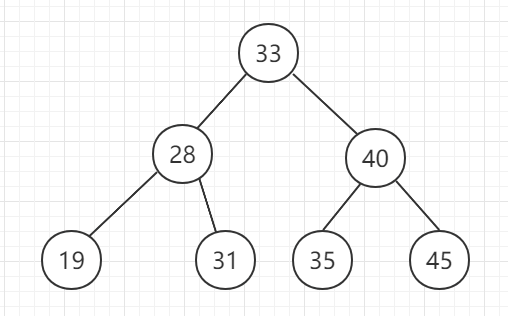
二分搜索树(英语:Binary Search Tree),也称为 二叉查找树 、二叉搜索树 、有序二叉树或排序二叉树。满足以下几个条件:
- 若它的左子树不为空,左子树上所有节点的值都小于它的根节点。
- 若它的右子树不为空,右子树上所有的节点的值都大于它的根节点。
它的左、右子树也都是二分搜索树。
如下图所示:
二、适用说明
二分搜索树有着高效的插入、删除、查询操作。
平均时间的时间复杂度为 O(log n),最差情况为 O(n)。二分搜索树与堆不同,不一定是完全二叉树,底层不容易直接用数组表示故采用链表来实现二分搜索树。
| 查找元素 | 插入元素 | 删除元素 | |
|---|---|---|---|
| 普通数组 | O(n) | O(n) | O(n) |
| 顺序数组 | O(logn) | O(n) | O(n) |
| 二分搜索树 | O(logn) | O(logn) | O(logn) |
下面先介绍数组形式的二分查找法作为思想的借鉴,后面继续介绍二分搜索树的查找方式。
三、二分查找法过程图示
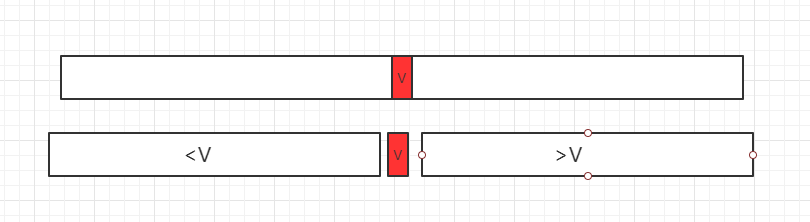
二分查找法的思想在 1946 年提出,查找问题是计算机中非常重要的基础问题,对于有序数列,才能使用二分查找法。如果我们要查找一元素,先看数组中间的值V和所需查找数据的大小关系,分三种情况:
- 1、等于所要查找的数据,直接找到
- 2、若小于 V,在小于 V 部分分组继续查询
- 2、若大于 V,在大于 V 部分分组继续查询
四、Java 实例代码
源码包下载:Download
src/runoob/binary/BinarySearch.java 文件代码:
package runoob.binarySearch;
/**
* 二分查找法
*/
public class BinarySearch {
// 二分查找法,在有序数组arr中,查找target
// 如果找到target,返回相应的索引index
// 如果没有找到target,返回-1
public static int find(Comparable[] arr, Comparable target) {
// 在arr[l...r]之中查找target
int l = 0, r = arr.length-1;
while( l <= r ){
//int mid = (l + r)/2;
// 防止极端情况下的整形溢出,使用下面的逻辑求出mid
int mid = l + (r-l)/2;
if( arr[mid].compareTo(target) == 0 )
return mid;
if( arr[mid].compareTo(target) > 0 )
r = mid - 1;
else
l = mid + 1;
}
return -1;
}
}
/**
* 二分查找法
*/
public class BinarySearch {
// 二分查找法,在有序数组arr中,查找target
// 如果找到target,返回相应的索引index
// 如果没有找到target,返回-1
public static int find(Comparable[] arr, Comparable target) {
// 在arr[l...r]之中查找target
int l = 0, r = arr.length-1;
while( l <= r ){
//int mid = (l + r)/2;
// 防止极端情况下的整形溢出,使用下面的逻辑求出mid
int mid = l + (r-l)/2;
if( arr[mid].compareTo(target) == 0 )
return mid;
if( arr[mid].compareTo(target) > 0 )
r = mid - 1;
else
l = mid + 1;
}
return -1;
}
}
备案号:闽ICP备20003806号 厦门市湖里区陈朝能网络技术工作室
 JsSaaS平台
JsSaaS平台